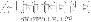
Let X1, X2, ... be independent, identically distributed random variable with P( Xj = 1 ) = q, P( Xj = -1 ) = 1-q
Let S0 = 0 and for n >= 1, Sn = X1 + X2 + ... + Xn. Let Yn = eSn
Let Y∞ = limn->∞(Yn)
Prove that Y∞ = 0
There are 2 ways to look into the problem. One is to consider log(Yn) and use the law of large number, the other way is that Yn+1/Yn does not converge with probability 1.
