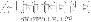In a simple setup, let's say (w₁, w₂) are weights invested in assets 1 and 2.

I only saw discussions when w₁+w₂=1, even if short selling is allowed.

Suppose I short the first asset and long the second one. My initial investment is 0.

What are the "weights" in this scenario?

0.5 for both. Note that we are taking the absolute value of the weights. It means that it should have been -0.5 (short) and +0.5 (long) such that they offset each other. However, we took |-0.5| = 0.5 (for the short position) for computation purposes.

Accademic people often analyze portfolios where there are an equal size long and short positions, so the weights add up to zero. Such portfolios are usually referred to as "arbitrage portfolios" or "zero net investment portfolios".

In real life, no broker will allow you to create such a position, you need to put up some cash to cover your potential losses. So for realistic analysis of an arbitrage strategy you have to decide how much cash (equity) you are going to put in. i.e. the degree of leverage you are willing to take. Only then would you be able to compute the actual returns an investment would make.

So there are two ways to analyze arbitrage portfolios, a simplified approach where the two weights add up to zero (usually seen in academic paper). Or a more realistic approach in which cash is also modeled and the three weights again add up to 1.